Educative example of parallel processing using threading on local computer, QSO from LSST AGN Data Challenge database

import QhX

from QhX import processing_utils

from QhX.processing_utils import parallel_pool,process_pool

This module provides functionality for parallel processing of data tasks using threading, on your local computer, if it is more handy than using our procedure for parallelization on High Performance Computer. This procedure could be used as an initial training for students.

Key Points:

Non-picklable Objects: Objects like DataManager that cannot be pickled (a requirement for multiprocessing) are handled efficiently using a threading approach (like with ThreadPool) because threads share the same memory space. This is particularly useful for objects that maintain state or have open connections (like database connections) that are not easily serialized.

I/O-Bound Tasks: For tasks that are I/O-bound (e.g., network data fetching, file reading, database querying), threading can significantly improve performance. While Python’s GIL (Global Interpreter Lock) prevents CPU-bound tasks from running in parallel in a multi-threaded environment, it allows I/O-bound tasks to execute concurrently.

Shared Resources: Threading is beneficial when using shared resources (like a shared DataManager instance) across different tasks without the need to initiate them separately for each task. Since all threads access the same memory space, a resource can be initialized once and used across all threads, enhancing memory efficiency.

CPU-Bound Tasks with GIL Limitations: Although threading in Python is not ideal for CPU-bound tasks due to the GIL, it can be advantageous for tasks that involve calling out to external applications or libraries that release the GIL (e.g., operations in NumPy, pandas, or I/O operations).

Rapid Task Switching Needs: Applications that benefit from rapid switching between tasks (e.g., handling multiple quick I/O operations concurrently) can leverage threading to facilitate this without the overhead of process creation and inter-process communication. “””

#import json
#import pandas as pd
#import numpy as np
#from sqlalchemy.engine import URL
from sqlalchemy.engine import create_engine
import matplotlib.pyplot as plt
import scipy
from scipy.optimize import curve_fit
from scipy.optimize import OptimizeWarning
from dateutil.relativedelta import relativedelta
import warnings
from itertools import groupby
import pyarrow as pa
import pyarrow.parquet as pq

## commonly used modules
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import os, sys
import yaml

pd.set_option('display.max_columns', 999)

from QhX.data_manager import DataManager
from QhX.detection import process1tiktok, process1, process1_new

class DataManager: “”” A class for managing and processing astronomical data sets.

This class provides methods to load and process forced source data and object data,
specifically focusing on time-domain objects and quasars.

Attributes
----------
fs_df : pd.DataFrame or None
    DataFrame containing forced source data.
fs_gp : pd.core.groupby.DataFrameGroupBy or None
    GroupBy object with forced source data grouped by object ID.
object_df : pd.DataFrame or None
    DataFrame containing object data.
td_objects : pd.DataFrame or None
    DataFrame containing time-domain objects.
"""

#This will take a time..

data_manager = DataManager()
fs_df = data_manager.load_fs_df('https://zenodo.org/record/6878414/files/ForcedSourceTable.parquet')
fs_gp = data_manager.group_fs_df()

INFO:root:Forced source data loaded successfully.
INFO:root:Forced source data grouped successfully.

td_objects=data_manager.load_object_df("https://zenodo.org/record/6878414/files/ObjectTable.parquet")
#Find quasars
setindexqso=td_objects[(td_objects["class"].eq("Qso"))].index

INFO:root:Object data loaded and processed successfully.

td_objects

	ra	dec	psPm_ra	psPm_dec	psParallax	psFlux_u	psFlux_g	psFlux_r	psFlux_i	psFlux_z	psFlux_y	psFluxErr_u	psFluxErr_g	psFluxErr_r	psFluxErr_i	psFluxErr_z	psFluxErr_y	bdFlux_u	bdFlux_g	bdFlux_r	bdFlux_i	bdFlux_z	bdFlux_y	bdFluxErr_u	bdFluxErr_g	bdFluxErr_r	bdFluxErr_i	bdFluxErr_z	bdFluxErr_y	psMag_u	psMag_g	psMag_r	psMag_i	psMag_z	psMag_y	psMagErr_u	psMagErr_g	psMagErr_r	psMagErr_i	psMagErr_z	psMagErr_y	bdMag_u	bdMag_g	bdMag_r	bdMag_i	bdMag_z	bdMag_y	bdMagErr_u	bdMagErr_g	bdMagErr_r	bdMagErr_i	bdMagErr_z	bdMagErr_y	extendedness_u	extendedness_g	extendedness_r	extendedness_i	extendedness_z	extendedness_y	stdColor_0	stdColor_1	stdColor_2	stdColor_3	stdColor_4	stdColorErr_0	stdColorErr_1	stdColorErr_2	stdColorErr_3	stdColorErr_4	class	photoZ_pest	z	flags_u	flags_g	flags_r	flags_i	flags_z	flags_y	spec_fiberid	spec_plate	spec_mjd	lcPeriodic[0]_g	lcPeriodic[0]_r	lcPeriodic[0]_i	lcPeriodic[1]_g	lcPeriodic[1]_r	lcPeriodic[1]_i	lcPeriodic[2]_g	lcPeriodic[2]_r	lcPeriodic[2]_i	lcPeriodic[3]_g	lcPeriodic[3]_r	lcPeriodic[3]_i	lcPeriodic[4]_u	lcPeriodic[4]_g	lcPeriodic[4]_r	lcPeriodic[4]_i	lcPeriodic[4]_z	lcPeriodic[5]_u	lcPeriodic[5]_g	lcPeriodic[5]_r	lcPeriodic[5]_i	lcPeriodic[5]_z	lcPeriodic[6]_u	lcPeriodic[6]_g	lcPeriodic[6]_r	lcPeriodic[6]_i	lcPeriodic[6]_z	lcPeriodic[7]_u	lcPeriodic[7]_g	lcPeriodic[7]_r	lcPeriodic[7]_i	lcPeriodic[7]_z	lcPeriodic[8]_u	lcPeriodic[8]_g	lcPeriodic[8]_r	lcPeriodic[8]_i	lcPeriodic[8]_z	lcPeriodic[9]_u	lcPeriodic[9]_g	lcPeriodic[9]_r	lcPeriodic[9]_i	lcPeriodic[9]_z	lcPeriodic[10]_u	lcPeriodic[10]_g	lcPeriodic[10]_r	lcPeriodic[10]_i	lcPeriodic[10]_z	lcPeriodic[11]_u	lcPeriodic[11]_g	lcPeriodic[11]_r	lcPeriodic[11]_i	lcPeriodic[11]_z	lcPeriodic[12]_u	lcPeriodic[12]_g	lcPeriodic[12]_r	lcPeriodic[12]_i	lcPeriodic[12]_z	lcPeriodic[13]_u	lcPeriodic[13]_g	lcPeriodic[13]_r	lcPeriodic[13]_i	lcPeriodic[13]_z	lcPeriodic[14]_u	lcPeriodic[14]_g	lcPeriodic[14]_r	lcPeriodic[14]_i	lcPeriodic[14]_z	lcPeriodic[15]_u	lcPeriodic[15]_g	lcPeriodic[15]_r	lcPeriodic[15]_i	lcPeriodic[15]_z	lcPeriodic[16]_u	lcPeriodic[16]_g	lcPeriodic[16]_r	lcPeriodic[16]_i	lcPeriodic[16]_z	lcPeriodic[17]_u	lcPeriodic[17]_g	lcPeriodic[17]_r	lcPeriodic[17]_i	lcPeriodic[17]_z	lcPeriodic[18]_u	lcPeriodic[18]_g	lcPeriodic[18]_r	lcPeriodic[18]_i	lcPeriodic[18]_z	lcPeriodic[19]_u	lcPeriodic[19]_g	lcPeriodic[19]_r	lcPeriodic[19]_i	lcPeriodic[19]_z	lcPeriodic[20]_u	lcPeriodic[20]_g	lcPeriodic[20]_r	lcPeriodic[20]_i	lcPeriodic[20]_z	lcPeriodic[21]_u	lcPeriodic[21]_g	lcPeriodic[21]_r	lcPeriodic[21]_i	lcPeriodic[21]_z	lcPeriodic[22]_u	lcPeriodic[22]_g	lcPeriodic[22]_r	lcPeriodic[22]_i	lcPeriodic[22]_z	lcPeriodic[23]_u	lcPeriodic[23]_g	lcPeriodic[23]_r	lcPeriodic[23]_i	lcPeriodic[23]_z	lcPeriodic[24]_u	lcPeriodic[24]_g	lcPeriodic[24]_r	lcPeriodic[24]_i	lcPeriodic[24]_z	lcPeriodic[25]_u	lcPeriodic[25]_g	lcPeriodic[25]_r	lcPeriodic[25]_i	lcPeriodic[25]_z	lcPeriodic[26]_u	lcPeriodic[26]_g	lcPeriodic[26]_r	lcPeriodic[26]_i	lcPeriodic[26]_z	lcPeriodic[27]_u	lcPeriodic[27]_g	lcPeriodic[27]_r	lcPeriodic[27]_i	lcPeriodic[27]_z	lcPeriodic[28]_u	lcPeriodic[28]_g	lcPeriodic[28]_r	lcPeriodic[28]_i	lcPeriodic[28]_z	lcPeriodic[29]_u	lcPeriodic[29]_g	lcPeriodic[29]_r	lcPeriodic[29]_i	lcPeriodic[29]_z	lcPeriodic[30]_u	lcPeriodic[30]_g	lcPeriodic[30]_r	lcPeriodic[30]_i	lcPeriodic[30]_z	lcPeriodic[31]_u	lcPeriodic[31]_g	lcPeriodic[31]_r	lcPeriodic[31]_i	lcPeriodic[31]_z	lcPeriodic[32]_u	lcPeriodic[32]_g	lcPeriodic[32]_r	lcPeriodic[32]_i	lcPeriodic[32]_z	lcNonPeriodic[0]_u	lcNonPeriodic[0]_g	lcNonPeriodic[0]_r	lcNonPeriodic[0]_i	lcNonPeriodic[0]_z	lcNonPeriodic[1]_u	lcNonPeriodic[1]_g	lcNonPeriodic[1]_r	lcNonPeriodic[1]_i	lcNonPeriodic[1]_z	lcNonPeriodic[2]_u	lcNonPeriodic[2]_g	lcNonPeriodic[2]_r	lcNonPeriodic[2]_i	lcNonPeriodic[2]_z	lcNonPeriodic[3]_u	lcNonPeriodic[3]_g	lcNonPeriodic[3]_r	lcNonPeriodic[3]_i	lcNonPeriodic[3]_z	lcNonPeriodic[4]_u	lcNonPeriodic[4]_g	lcNonPeriodic[4]_r	lcNonPeriodic[4]_i	lcNonPeriodic[4]_z	lcNonPeriodic[5]_u	lcNonPeriodic[5]_g	lcNonPeriodic[5]_r	lcNonPeriodic[5]_i	lcNonPeriodic[5]_z	lcNonPeriodic[6]_u	lcNonPeriodic[6]_g	lcNonPeriodic[6]_r	lcNonPeriodic[6]_i	lcNonPeriodic[6]_z	lcNonPeriodic[7]_u	lcNonPeriodic[7]_g	lcNonPeriodic[7]_r	lcNonPeriodic[7]_i	lcNonPeriodic[7]_z	lcNonPeriodic[8]_u	lcNonPeriodic[8]_g	lcNonPeriodic[8]_r	lcNonPeriodic[8]_i	lcNonPeriodic[8]_z	lcNonPeriodic[9]_u	lcNonPeriodic[9]_g	lcNonPeriodic[9]_r	lcNonPeriodic[9]_i	lcNonPeriodic[9]_z	lcNonPeriodic[10]_u	lcNonPeriodic[10]_g	lcNonPeriodic[10]_r	lcNonPeriodic[10]_i	lcNonPeriodic[10]_z	lcNonPeriodic[11]_u	lcNonPeriodic[11]_g	lcNonPeriodic[11]_r	lcNonPeriodic[11]_i	lcNonPeriodic[11]_z	lcNonPeriodic[12]_u	lcNonPeriodic[12]_g	lcNonPeriodic[12]_r	lcNonPeriodic[12]_i	lcNonPeriodic[12]_z	lcNonPeriodic[13]_u	lcNonPeriodic[13]_g	lcNonPeriodic[13]_r	lcNonPeriodic[13]_i	lcNonPeriodic[13]_z	lcNonPeriodic[14]_u	lcNonPeriodic[14]_g	lcNonPeriodic[14]_r	lcNonPeriodic[14]_i	lcNonPeriodic[14]_z	lcNonPeriodic[15]_u	lcNonPeriodic[15]_g	lcNonPeriodic[15]_r	lcNonPeriodic[15]_i	lcNonPeriodic[15]_z	lcNonPeriodic[16]_u	lcNonPeriodic[16]_g	lcNonPeriodic[16]_r	lcNonPeriodic[16]_i	lcNonPeriodic[16]_z	lcNonPeriodic[17]_u	lcNonPeriodic[17]_g	lcNonPeriodic[17]_r	lcNonPeriodic[17]_i	lcNonPeriodic[17]_z	lcNonPeriodic[18]_u	lcNonPeriodic[18]_g	lcNonPeriodic[18]_r	lcNonPeriodic[18]_i	lcNonPeriodic[18]_z	lcNonPeriodic[19]_u	lcNonPeriodic[19]_g	lcNonPeriodic[19]_r	lcNonPeriodic[19]_i	lcNonPeriodic[19]_z	lcNonPeriodic[20]_u	lcNonPeriodic[20]_g	lcNonPeriodic[20]_r	lcNonPeriodic[20]_i	lcNonPeriodic[20]_z	lcNonPeriodic[21]_u	lcNonPeriodic[21]_g	lcNonPeriodic[21]_r	lcNonPeriodic[21]_i	lcNonPeriodic[21]_z	lcNonPeriodic[22]_u	lcNonPeriodic[22]_g	lcNonPeriodic[22]_r	lcNonPeriodic[22]_i	lcNonPeriodic[22]_z	lcNonPeriodic[23]_u	lcNonPeriodic[23]_g	lcNonPeriodic[23]_r	lcNonPeriodic[23]_i	lcNonPeriodic[23]_z	lcNonPeriodic[24]_u	lcNonPeriodic[24]_g	lcNonPeriodic[24]_r	lcNonPeriodic[24]_i	lcNonPeriodic[24]_z	lcNonPeriodic[25]_u	lcNonPeriodic[25]_g	lcNonPeriodic[25]_r	lcNonPeriodic[25]_i	lcNonPeriodic[25]_z	lcNonPeriodic[26]_u	lcNonPeriodic[26]_g	lcNonPeriodic[26]_r	lcNonPeriodic[26]_i	lcNonPeriodic[26]_z	lcNonPeriodic[27]_u	lcNonPeriodic[27]_g	lcNonPeriodic[27]_r	lcNonPeriodic[27]_i	lcNonPeriodic[27]_z	lcNonPeriodic[28]_u	lcNonPeriodic[28]_g	lcNonPeriodic[28]_r	lcNonPeriodic[28]_i	lcNonPeriodic[28]_z	ebv
objectId
0271388	359.99169	0.969968	NaN	NaN	NaN	26160.979422	294519.269238	1.106956e+06	2.057265e+06	2.982015e+06	NaN	300.738260	256.142174	488.893498	770.129959	2161.119294	NaN	26436.085624	294967.193358	1.116087e+06	2.086941e+06	3.014907e+06	NaN	337.760680	919.045860	3311.546956	6004.226909	8854.073234	NaN	20.27555	17.727280	16.289740	15.616840	15.253790	NaN	0.012473	0.000944	0.000480	0.000406	0.000787	NaN	20.26420	17.725630	16.280820	15.601290	15.241880	NaN	0.013862	0.003383	0.003221	0.003124	0.003189	NaN	0.0	0.000000	0.000000	0.000000	0.000000	NaN	2.628649	1.437541	0.672900	0.403049	NaN	0.012517	0.001059	0.000629	0.000886	NaN	Star	NaN	0.000000	0	0.0	0.0	0.0	0.0	<NA>	444	1489	52991	0.260275	0.061273	0.705092	21803.405141	276794.642597	1.777113e+04	16.228020	15.676071	948.808741	7408.387338	8196.866826	109911.497814	0.063015	0.029211	0.028178	0.021458	0.022473	0.006836	0.004464	0.002411	0.001684	0.001341	0.000797	0.000194	0.000458	0.000116	0.000499	0.000257	0.000151	0.000112	0.000153	0.000144	17.793201	20.851046	25.465177	25.805538	31.382942	-1.200072	1.414476	2.535535	1.719811	-1.038697	-1.765356	3.044971	-1.770712	-2.701489	-2.897284	2.583548	1.189083	0.597592	-2.033987	3.085672	0.055051	0.024847	1.994609e-02	0.022730	0.019042	0.000698	0.001973	0.001522	0.002482	0.001308	0.000547	0.000563	0.000196	0.000696	0.000543	0.000272	0.000116	0.000101	0.000091	0.000115	7.033954	10.586698	22.454945	14.203220	19.134806	1.692748	1.862281	1.350974	2.605782	-2.856124	-2.747079	2.611592	-2.579242	-3.095433	-0.208689	0.366546	-1.783012	-1.453997	0.094679	1.152248	0.050092	0.023383	1.976994e-02	0.016176	0.014899	0.006944	0.001797	0.001319	0.000316	0.001818	0.000572	0.000338	0.000309	0.000396	0.000479	0.000524	0.000060	0.000049	0.000077	0.000039	8.662116	19.452124	21.457851	28.781258	8.571919	-0.630059	1.376486	1.326487	1.490568	2.937560	-1.411466	0.931117	2.832502	-2.357249	-2.218536	-1.395257	1.561549	-2.367043	-0.548603	-1.384439	3.248688	2.795955	1.698663	2.758158	3.376963	1.065883	1.012299	0.980038	1.052691	0.972465	1.022609	1.170294	1.020969	1.009958	0.968035	0.000017	0.000005	0.000026	0.000005	0.000003	0.007866	-0.004576	-0.004189	-0.000083	0.000362	0.295908	0.133103	0.446917	0.157799	0.076649	0.396552	0.092593	0.163636	0.129630	0.272727	0.193276	0.063699	0.076586	0.157090	0.131541	0.328259	0.096179	0.158223	0.232468	0.223962	0.438685	0.147633	0.261800	0.456678	0.384206	0.597733	0.238137	0.470788	0.558575	0.478881	0.860509	0.320848	0.707844	0.765057	0.719575	-3.960000e-06	-0.000024	-0.000032	-0.000004	-0.000010	0.204516	0.109223	0.160211	0.106130	0.103399	0.075589	0.011327	0.012177	0.017920	0.018605	0.327586	0.833333	0.981818	0.796296	0.454545	0.033333	-0.100000	-0.033333	-0.033333	-0.100000	0.296377	0.232779	1.152342	0.252554	0.076061	0.328733	0.138596	0.081416	0.075083	0.108642	0.299422	0.948320	1.646192	0.927857	0.673444	0.427606	0.207382	1.427587	0.182553	-0.043269	0.577648	-3.045336	-6.682989	-3.372514	0.098978	0.341046	10.872827	51.567125	21.372289	-0.027995	0.120161	0.048099	0.113966	0.041830	0.034588	0.032831	-0.833647	-0.796085	-0.904402	-0.932227	1.009285	0.645986	0.358198	0.722727	0.995394	2.435431	3.296827	2.019703	3.457908	3.751185	1.714467	6.544237	7.264410	6.807538	4.043939	-0.000436	0.001919	0.012756	0.001517	0.000796	-2.000000e-08	1.100000e-07	8.800000e-07	1.200000e-07	6.000000e-08	0.154169	0.175675	0.131685	0.145041	0.141396	2.345330	1.454206	2.029815	1.717249	2.059443	0.029877	0.032109	0.030674	0.062576	0.324707	8.555394	2.888606	0.961880	1.213456	0.034117	0.023638
0271389	359.98092	0.652865	NaN	NaN	NaN	48849.324901	77854.298779	7.187044e+04	6.333212e+04	5.460789e+04	NaN	291.531809	136.426346	155.161709	222.153745	687.840468	NaN	49320.945937	78824.057129	7.230736e+04	6.410164e+04	5.491608e+04	NaN	355.036831	280.727554	302.808418	344.397471	765.829936	NaN	19.59781	19.171840	19.258650	19.395890	19.594210	NaN	0.006478	0.001902	0.002344	0.003808	0.013608	NaN	19.58738	19.158400	19.252070	19.382780	19.588130	NaN	0.007814	0.003867	0.004547	0.005832	0.015066	NaN	0.0	0.000000	0.000000	0.000000	0.000000	NaN	0.506060	-0.086831	-0.137316	-0.160921	NaN	0.006753	0.003019	0.004472	0.014196	NaN	Star	NaN	0.000000	0	0.0	0.0	0.0	0.0	<NA>	464	685	52203	0.027656	0.056467	0.033964	3894.407106	6726.629772	2.815442e+03	0.966700	13395.881279	428.826473	400.979284	733.893590	537.121360	0.085759	0.027452	0.024536	0.030410	0.091534	0.005756	0.004097	0.002611	0.001179	0.011236	0.001800	0.000134	0.000690	0.001046	0.002691	0.000384	0.000304	0.000188	0.000153	0.001317	31.360928	25.385482	8.506283	26.412038	4.506639	2.594933	1.812034	2.417874	0.493405	0.927162	-2.036974	-3.085754	-2.850238	-1.593147	2.303191	0.865115	-0.928600	-0.794408	2.780938	-2.871577	0.083625	0.020436	2.021357e-02	0.020953	0.061363	0.014543	0.002019	0.000681	0.000275	0.000964	0.002079	0.000265	0.000314	0.000103	0.002567	0.000707	0.000022	0.000079	0.000092	0.000249	6.800123	25.915992	13.872531	29.464400	9.975824	1.694027	-0.370578	1.951843	-1.944132	0.379092	-2.421081	1.421683	0.794701	1.141263	2.694204	0.197027	-0.861673	-1.568726	0.471050	-1.056306	0.070105	0.016609	1.751555e-02	0.018027	0.052373	0.006444	0.001955	0.001570	0.001223	0.002532	0.001194	0.000441	0.000192	0.000215	0.000921	0.000412	0.000142	0.000151	0.000013	0.000391	7.311038	30.640375	24.474704	17.710612	16.832298	1.350979	2.061168	1.344819	2.401992	-1.225512	3.088658	2.000862	2.508822	0.383284	0.818757	-1.426423	-0.271237	-1.739701	-1.816670	1.199842	3.115335	3.339667	3.575351	3.704359	3.271407	1.038554	1.017902	0.964577	0.978190	1.021438	1.078696	1.018579	0.977984	1.025239	0.997379	0.000043	0.000003	0.000003	0.000003	0.000026	-0.005620	-0.005796	0.000470	-0.000590	-0.003786	0.470875	0.113661	0.097450	0.088941	0.382093	0.118644	0.196721	0.311475	0.377049	0.254237	0.094119	0.133534	0.188502	0.106396	0.131925	0.171574	0.248519	0.264787	0.279666	0.204191	0.334130	0.355460	0.370550	0.465098	0.293789	0.513566	0.484704	0.528046	0.523567	0.387523	0.748043	0.633131	0.693800	0.724698	0.707084	-9.300000e-06	-0.000002	0.000016	0.000011	0.000002	0.335029	0.053404	0.048027	0.141555	0.213026	0.050968	0.020456	0.024292	0.033302	0.056990	0.677966	0.590164	0.360656	0.327869	0.644068	0.033333	0.100000	0.033333	-0.033333	0.033333	0.892854	0.168879	0.106714	0.093059	0.661470	0.287679	0.105503	0.117048	0.131128	0.352213	2.283128	0.312337	0.407321	0.279854	0.761498	-0.054771	-0.019150	0.027962	0.077000	0.119618	-2.512992	-1.485583	-0.249957	-0.130027	-1.473776	11.186223	5.342639	0.405382	-0.315281	5.568996	0.147088	0.037726	0.038699	0.041392	0.127224	-0.114619	-0.895329	-0.900965	-0.897053	-0.149659	0.742126	0.895528	0.993488	1.003835	0.849841	1.946030	3.610405	3.614440	3.542608	2.203727	15.766159	2.508530	3.038078	2.029591	2.644706	0.019628	0.000696	0.000920	0.000915	0.009523	8.700000e-07	3.000000e-08	4.000000e-08	4.000000e-08	4.200000e-07	0.120839	0.168678	0.187505	0.128585	0.158396	2.126834	2.225141	2.210442	2.186761	2.023726	0.058902	0.242187	0.034497	0.210657	0.145120	4.915713	0.018316	1.949530	0.051217	0.686231	0.027264
0271390	359.97467	-1.066557	14.123035	-6.600603	-0.013308	58226.877642	196208.333415	3.151411e+05	3.634721e+05	3.904259e+05	386038.526191	336.538277	176.139373	238.635004	284.737560	391.672093	1157.866247	57822.261087	193323.677945	3.125762e+05	3.612207e+05	3.864206e+05	377835.751201	414.728788	168.305007	250.304491	379.888888	572.420765	1887.447062	19.40718	18.168272	17.653803	17.498888	17.421219	17.433489	0.006274	0.000974	0.000822	0.000850	0.001089	0.003252	19.41475	18.184353	17.662676	17.505634	17.432415	17.456808	0.007786	0.000945	0.000869	0.001141	0.001607	0.005410	0.0	0.011742	0.002451	0.008652	0.012358	0.144320	1.318985	0.514469	0.154915	0.077669	-0.012270	0.006351	0.001275	0.001183	0.001382	0.003434	Star	NaN	0.000000	0	0.0	0.0	0.0	0.0	0	114	1091	52902	0.147567	0.027901	0.081723	10795.856574	18759.841927	3.118562e+02	7234.038051	288.249310	0.745502	2782.532404	1216.675112	4025.346049	0.067701	0.031648	0.017832	0.028988	0.034787	0.002850	0.002975	0.003410	0.003147	0.002162	0.001387	0.000799	0.000353	0.000465	0.000747	0.000472	0.000250	0.000268	0.000185	0.000182	16.622884	3.013541	22.457930	11.419543	29.008176	1.256466	1.731638	2.800763	1.082790	1.004401	2.158424	-2.381636	-0.861027	2.246314	-2.231599	-1.982340	-0.686695	-0.301330	-2.434347	0.500951	0.054560	0.027086	1.305491e-02	0.026558	0.023021	0.005701	0.002115	0.000636	0.002372	0.000847	0.001061	0.000474	0.000286	0.000573	0.000245	0.000239	0.000142	0.000090	0.000160	0.000079	3.542381	11.262393	16.766711	1.002731	18.488068	2.511450	0.822600	-0.387496	1.538420	1.800560	-2.437052	2.612016	2.802031	1.935085	-1.326998	1.123629	-1.814400	-2.955947	-2.598134	-2.419319	0.047071	0.024947	1.032311e-02	0.135437	0.018668	0.000975	0.001139	0.000694	0.106774	0.000660	0.000917	0.000430	0.000295	0.087695	0.000212	0.000212	0.000118	0.000047	0.050082	0.000097	29.974516	1.373557	18.824192	13.563423	32.377205	0.261512	0.113457	-0.051408	1.551414	-0.505649	1.837342	1.717850	1.921156	3.026279	0.678476	2.713529	2.706397	2.636471	-1.779049	-1.122446	2.815443	2.719889	3.179630	1.926369	3.639889	0.993550	1.005041	0.980678	0.995311	0.896094	0.977483	1.025819	0.940343	1.459028	0.956949	0.000029	0.000009	0.000001	0.000020	0.000003	-0.005754	-0.003722	-0.003744	-0.004045	-0.000761	0.489872	0.222805	0.083009	0.320217	0.119581	0.240741	0.094340	0.230769	0.020000	0.226415	0.127227	0.061580	0.129417	0.174800	0.103412	0.207557	0.111888	0.240844	0.298839	0.185875	0.270546	0.201269	0.371345	0.484824	0.274378	0.432633	0.397461	0.516446	0.601171	0.413986	0.633878	0.638186	0.707457	0.803790	0.543017	1.830000e-05	0.000010	-0.000003	-0.000002	-0.000016	0.211109	0.196668	0.047228	0.295708	0.121199	0.049787	0.015057	0.011363	0.013417	0.018822	0.759259	0.811321	0.673077	0.980000	0.603774	0.166667	0.033333	0.100000	0.033333	0.100000	0.949866	0.394289	0.124178	0.728577	0.129292	0.306527	0.130465	0.060069	0.060807	0.136541	1.815737	1.664602	-0.556924	2.420012	0.664704	0.424288	-0.127063	0.786323	0.056595	0.075107	-2.717639	-3.444700	-2.252920	-6.284135	-0.536066	12.020285	18.935806	8.454215	46.368981	1.952474	0.152410	0.062654	0.028283	0.085349	0.042963	-0.156624	-0.795743	-0.926226	-0.841389	-0.848115	0.714381	0.651424	0.807338	0.410812	0.900022	1.880220	2.968701	3.921625	2.463289	3.495311	8.853320	12.134792	1.613586	18.479451	3.874493	0.020923	0.003521	0.000307	0.007081	0.001361	1.020000e-06	2.000000e-07	2.000000e-08	4.600000e-07	8.000000e-08	0.178565	0.188643	0.171811	0.141249	0.147907	1.258739	1.690556	1.657900	2.058601	2.193501	0.170739	0.018121	0.008570	0.057029	0.042912	0.975324	5.251484	6.415285	0.447885	1.378181	0.039193
0271391	359.97300	0.203557	9.591976	-3.451329	-0.012580	56604.337841	137549.637098	1.816154e+05	1.948576e+05	1.999601e+05	192414.700415	373.645494	142.514416	153.336214	181.999459	276.628670	1173.991063	56216.171259	135464.359811	1.799253e+05	1.923424e+05	1.964709e+05	189718.747536	449.633549	152.372613	182.104973	277.541501	514.453020	1981.721606	19.43786	18.553917	18.252184	18.175772	18.147707	18.189470	0.007166	0.001124	0.000916	0.001014	0.001501	0.006604	19.44533	18.570503	18.262335	18.189878	18.166820	18.204790	0.008683	0.001221	0.001098	0.001566	0.002839	0.011282	0.0	0.016235	0.007502	0.013772	0.015777	0.412266	0.964024	0.301733	0.076412	0.028065	-0.041763	0.007255	0.001451	0.001367	0.001812	0.006793	Star	NaN	0.000000	0	0.0	0.0	0.0	0.0	0	690	4216	55477	0.330060	0.686030	1.141392	5866.936189	51241.893766	3.849883e+00	3.183538	308.397120	0.621720	5660.780677	5182.637331	8120.975846	0.072021	0.039824	0.025629	0.028717	0.034787	0.009823	0.007883	0.002304	0.002474	0.005400	0.001113	0.000842	0.000285	0.000570	0.000577	0.000115	0.000252	0.000090	0.000089	0.000064	18.783281	20.851171	9.026542	31.480394	21.203211	2.828571	1.721295	2.187130	0.934707	-2.187591	-1.429864	-2.625213	-1.967833	2.696984	-1.095929	-0.829054	-0.810167	0.807612	-2.423306	3.076315	0.056650	0.030470	2.000000e-08	0.025418	0.024585	0.004618	0.004062	0.000000	0.002349	0.000409	0.001146	0.000848	0.000000	0.000569	0.000278	0.000086	0.000220	0.000000	0.000081	0.000076	2.619925	30.574655	2.016725	0.888059	6.961652	1.135364	2.267121	-0.102280	0.900112	0.505213	2.997585	-2.122545	-0.269059	2.314287	1.987972	-2.230700	-0.395149	-0.379588	-2.959296	0.889247	0.045785	0.025396	2.000000e-08	0.024321	0.019093	0.004335	0.001419	0.000000	0.002334	0.001279	0.001487	0.000546	0.000000	0.000516	0.000238	0.000166	0.000041	0.000000	0.000111	0.000057	29.118797	15.714504	2.016725	4.513138	23.442467	1.248861	1.702365	-0.102280	1.466597	0.540395	-1.982699	-2.967618	-0.269060	1.758336	-1.238976	2.807839	3.028002	-0.379589	3.115840	1.623746	3.544123	3.252194	1.850075	2.504960	4.088142	0.990121	1.036413	0.938706	0.957584	0.918261	0.975472	0.937877	0.938706	0.957504	0.833768	0.000027	0.000010	0.000031	0.000016	0.000005	-0.000568	-0.003769	0.000161	-0.004443	0.005301	0.425307	0.202355	0.585855	0.345649	0.131723	0.230769	0.108108	0.064935	0.105263	0.341772	0.118754	0.079685	0.116909	0.115084	0.150143	0.204306	0.122447	0.239926	0.213198	0.342260	0.341930	0.210397	0.355669	0.318284	0.435951	0.529842	0.319669	0.581774	0.440591	0.569840	0.687036	0.526640	0.792478	0.644410	0.776247	-1.154000e-05	-0.000012	-0.000033	0.000001	-0.000016	0.773506	0.323535	0.220584	0.239068	0.151695	0.067451	0.017444	0.017298	0.020123	0.035212	0.576923	0.743243	0.987013	0.934211	0.417722	0.100000	0.033333	0.100000	0.033333	0.100000	0.622016	0.344113	1.745732	0.771946	0.152362	0.337687	0.167918	0.084868	0.111526	0.152522	1.764003	1.631945	2.203572	2.224472	0.278115	0.063463	0.305433	1.261965	0.157909	0.357657	-0.790781	-2.921025	-7.921338	-6.036430	0.776552	4.203597	10.245625	70.685035	47.787457	0.633229	0.125892	0.070536	0.127315	0.079078	0.054391	-0.081350	-0.755989	-0.794709	-0.810022	-0.785029	0.881693	0.660619	0.353309	0.534103	0.998008	2.265797	2.843115	1.751516	2.568464	3.281653	7.321677	9.028815	12.637098	14.650283	2.209808	0.011105	0.004588	0.016063	0.005962	0.001299	3.700000e-07	1.800000e-07	6.200000e-07	2.400000e-07	5.000000e-08	0.078550	0.147950	0.110191	0.132400	0.173646	2.464347	1.702623	2.105601	1.771717	1.809222	0.183350	0.055463	0.165852	0.318518	0.027876	0.441824	2.040820	0.051330	0.018316	5.699177	0.033451
0271392	359.97109	-1.007636	4.124890	-3.065300	NaN	-69224.617745	1871.996571	7.629826e+03	2.748630e+04	4.817328e+04	55599.520852	42669.094349	81.535894	89.749332	152.700499	267.518464	1133.339315	-83064.453315	1577.575848	7.479136e+03	2.677157e+04	4.667340e+04	54018.167714	43381.628696	114.878110	175.594532	302.844986	521.101272	1765.992681	NaN	23.219303	21.693779	20.302275	19.693050	19.537388	NaN	0.046289	0.012697	0.006015	0.006013	0.021909	NaN	23.405090	21.715437	20.330881	19.727392	19.568716	NaN	0.076317	0.025196	0.012213	0.012055	0.034928	0.0	0.398209	0.019596	0.016319	0.016609	0.090982	NaN	1.525524	1.391504	0.609225	0.155662	0.670901	0.048984	0.014124	0.008529	0.022938	Star	NaN	0.000000	0	0.0	0.0	0.0	0.0	0	646	7850	56956	0.000001	NaN	0.000016	341.703289	NaN	3.264001e+06	0.043432	NaN	0.000040	0.574150	NaN	1.883511	1.757934	0.294156	0.077142	0.035747	0.099399	0.225284	0.021059	0.003966	0.002971	0.001661	0.025566	0.002426	0.000775	0.001049	0.001634	0.015874	0.002977	0.000154	0.000144	0.000465	16.708076	2.524494	18.664030	17.869122	8.970319	0.917918	2.527558	-0.675472	2.212460	-2.728763	2.383380	2.937249	-1.955872	1.790559	-0.552392	-0.998204	2.553825	1.641681	3.062710	-2.283831	0.873789	0.158361	4.533017e-02	0.024517	0.076980	0.070861	0.003599	0.002462	0.001179	0.002563	0.013577	0.001363	0.000466	0.000353	0.000188	0.005209	0.000419	0.000167	0.000181	0.001084	6.411031	23.386809	7.743794	31.375025	11.668926	-2.988122	-0.815338	-2.984790	2.964469	-0.854343	-2.656093	1.322262	2.547645	-2.256767	2.175672	2.771855	1.922124	0.936027	-0.181931	-1.753289	0.460523	0.107227	3.478447e-02	0.015969	0.043055	0.008874	0.006299	0.001635	0.003527	0.003922	0.004276	0.002069	0.000526	0.000459	0.000682	0.001207	0.000387	0.000081	0.000051	0.000159	25.100701	31.868194	6.817927	17.806417	28.465528	0.674840	-2.196680	1.571518	1.181693	-0.132410	2.846809	-3.070055	0.812856	2.420456	2.135098	2.883993	0.569111	-0.930729	1.520266	3.042030	3.410817	3.128307	2.901965	2.764474	2.907295	0.928470	0.964422	0.925130	1.122049	1.021980	0.873569	0.934536	0.933027	0.988702	0.947101	0.001377	0.000070	0.000007	0.000002	0.000014	0.197956	0.054935	0.001537	-0.007648	-0.000296	2.646619	0.839132	0.244440	0.089064	0.290756	0.258065	0.322581	0.387097	0.310345	0.322581	0.353973	0.084383	0.108346	0.125094	0.094702	0.398541	0.186532	0.242903	0.351733	0.213687	0.455104	0.325647	0.365755	0.481068	0.279687	0.558285	0.542239	0.505460	0.559565	0.601512	0.751585	0.642372	0.710756	0.679114	0.845909	-4.479500e-04	0.000171	-0.000014	-0.000004	-0.000050	1.400618	0.326454	0.092420	0.072053	0.130406	1.239994	0.188972	0.050531	0.024632	0.046085	0.096774	0.483871	0.483871	0.310345	0.516129	0.033333	0.100000	0.033333	0.066667	-0.100000	19.184174	0.948554	0.265660	0.120710	0.348656	7.085468	1.140939	0.287209	0.105975	0.293619	1.883783	-0.166083	-0.510187	-0.983182	0.097728	-0.359071	0.246605	0.276920	0.006163	0.095525	-0.105579	0.536360	1.084132	-0.978634	-0.177473	-1.112887	1.526219	2.060896	1.783666	1.754256	1.412473	0.365416	0.105394	0.038795	0.112456	14.316072	2.164092	-0.216810	-0.885184	-0.104464	0.985680	0.916667	0.915624	0.973869	0.910155	-1.453326	1.147363	2.604155	3.591221	2.437603	6.818414	0.938055	0.718650	0.524245	1.461340	1.618950	-0.080069	-0.001857	-0.001143	0.003822	8.864000e-05	-4.800000e-06	-1.300000e-07	-9.000000e-08	3.200000e-07	0.174398	0.238544	0.209646	0.220836	0.180493	2.228439	2.023039	2.546435	2.395137	1.886600	0.330013	0.006272	0.000009	0.000001	0.013985	35.063518	1695.317980	0.897756	61.433233	10.639567	0.042526
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
1468017	309.23870	0.028991	-0.662283	0.020786	0.442488	17994.203485	27268.917052	3.142641e+04	4.412361e+04	6.025053e+04	NaN	840.888061	330.659188	453.818901	635.652520	2865.202526	NaN	20141.763745	31723.140172	3.907511e+04	5.721970e+04	7.828750e+04	NaN	1033.235168	421.199788	592.484241	831.089567	3661.875674	NaN	20.68143	20.310740	20.156620	19.788150	19.487930	NaN	0.050663	0.013162	0.015673	0.015634	0.051420	NaN	20.55918	20.146510	19.920180	19.506060	19.204510	NaN	0.055630	0.014413	0.016459	0.015766	0.050661	NaN	0.0	0.000000	1.000000	1.000000	1.000000	NaN	0.451338	0.154067	0.368441	0.338225	NaN	0.052418	0.020473	0.022147	0.053949	NaN	Qso	NaN	0.442569	0	0.0	0.0	0.0	0.0	<NA>	301	1117	52885	0.001658	157.665964	1.686491	11808.289927	2.918011	1.166877e-01	0.226252	53990.898110	1772.358819	216.197917	34060.346688	4252.394697	0.118145	0.066106	0.079768	0.074369	0.109995	0.007012	0.008669	0.005027	0.007341	0.010261	0.001312	0.001222	0.001648	0.000830	0.003015	0.001328	0.000461	0.000621	0.000613	0.001291	23.943282	30.005356	6.535160	26.240096	18.299638	1.115732	1.453053	1.591550	2.604331	0.743958	1.147619	-2.508004	0.947574	0.003693	0.162353	-2.652867	-2.011022	0.535263	0.873255	-0.056988	0.071870	0.056238	5.555584e-02	0.057301	0.069779	0.004924	0.005322	0.002752	0.004854	0.003771	0.001614	0.001562	0.000053	0.000679	0.000398	0.000557	0.000256	0.000489	0.000200	0.000164	29.119755	21.753474	18.017381	16.011315	9.136434	-0.298428	2.022570	-0.344032	2.578638	1.078315	2.770159	-1.996590	-1.138063	-1.161240	-2.449204	-0.344762	1.220506	0.959394	2.167365	0.014427	0.067934	0.039770	4.482285e-02	0.048003	0.063702	0.010151	0.002060	0.002563	0.008099	0.002484	0.000642	0.000710	0.000211	0.002289	0.002021	0.000507	0.000112	0.000129	0.000554	0.000090	30.991141	18.139023	1.844936	21.053356	10.944690	2.093385	-2.237273	0.434765	2.893095	-1.321719	-2.810590	-0.499360	1.114431	2.455773	1.428864	2.546075	1.816015	1.573900	1.888571	-2.903962	3.506426	3.088294	3.312144	3.352258	3.460452	0.923960	1.117644	0.963872	1.007617	0.935207	0.999937	0.984851	0.973749	0.961108	0.945413	0.000021	0.000013	0.000014	0.000014	0.000025	-0.010464	-0.008751	-0.011574	-0.001052	-0.020184	0.273651	0.272655	0.235620	0.217542	0.296439	0.377778	0.181818	0.244444	0.400000	0.340909	0.188373	0.068371	0.110770	0.322155	0.157569	0.303714	0.144456	0.216280	0.466907	0.210557	0.436121	0.242260	0.376974	0.609195	0.337661	0.599003	0.305606	0.544107	0.719546	0.484839	0.903266	0.407209	0.731029	0.849745	0.621334	1.100000e-07	0.000049	-0.000013	-0.000012	-0.000029	0.257301	0.193310	0.139174	0.123630	0.175040	0.084204	0.047152	0.065647	0.085737	0.102103	0.222222	0.568182	0.400000	0.222222	0.409091	0.033333	-0.033333	-0.166667	0.166667	-0.100000	0.279530	0.470031	0.330856	0.224588	0.383073	0.412698	0.345072	0.298856	0.256603	0.480791	-0.029264	0.994183	1.560730	1.483853	0.470530	0.415394	1.104482	0.322692	0.431435	0.186821	-0.177306	-1.848359	-0.767855	0.231027	-0.377397	-0.552926	5.457899	0.931366	-0.568896	0.113247	0.138410	0.103095	0.098554	0.100866	0.140055	0.302686	-0.425686	-0.280287	-0.108967	0.295360	1.029259	0.798986	0.953401	1.095929	1.003425	2.209172	2.430920	2.547728	2.603851	2.167458	1.697063	15.348310	11.516030	10.826588	2.135317	0.002383	0.009607	0.009015	0.009300	0.010184	1.200000e-07	5.300000e-07	4.900000e-07	5.300000e-07	6.100000e-07	0.166675	0.182525	0.234406	0.208505	0.209825	1.742694	1.620858	1.626095	1.749285	1.639964	0.014565	0.022847	0.078444	0.062067	0.084517	87.726218	40.008760	2.298066	4.310347	2.627439	0.085374
1468018	309.22960	0.171063	0.532933	-0.023733	0.517200	58302.017211	61925.019907	6.830879e+04	6.212039e+04	6.179836e+04	NaN	1013.180546	386.147718	510.050231	638.044346	2865.021901	NaN	57662.689860	62019.204528	6.851232e+04	6.237270e+04	6.194137e+04	NaN	1117.087553	461.317152	596.951683	728.222725	3003.253467	NaN	19.40578	19.420370	19.313830	19.416860	19.460500	NaN	0.018865	0.006770	0.008106	0.011149	0.050139	NaN	19.41775	19.418720	19.310600	19.412460	19.458000	NaN	0.021031	0.008076	0.009459	0.012674	0.052438	NaN	0.0	0.000000	0.000000	0.000000	0.000000	NaN	0.065456	0.106526	-0.103106	-0.005643	NaN	0.020046	0.010562	0.013787	0.051556	NaN	Qso	NaN	1.110641	0	0.0	0.0	0.0	0.0	<NA>	354	1117	52885	1.897691	0.800918	0.536513	0.004062	0.004426	4.191075e-03	841.379095	441.405419	277.195879	6571.325342	1354.693991	1703.822432	0.205902	0.179013	0.117750	0.108634	0.088397	0.033625	0.014283	0.021411	0.010015	0.008837	0.003459	0.002366	0.004247	0.002206	0.001636	0.001910	0.000971	0.001618	0.000568	0.000181	0.001085	0.001085	0.001085	0.001085	12.239978	-2.609709	2.912295	-2.736895	-2.947658	-2.129578	0.711405	1.109920	1.452175	1.844308	0.110901	-2.633205	2.850055	3.136856	-3.086786	0.423779	0.077102	0.046874	2.834943e-02	0.032937	0.056822	0.002598	0.002730	0.001884	0.004968	0.003657	0.002219	0.001365	0.000642	0.000361	0.000275	0.000428	0.000237	0.000086	0.000188	0.000559	6.398674	28.530733	15.927267	21.217587	4.722602	-0.255515	2.598775	-0.267996	-2.595866	-2.038785	2.591071	3.041575	0.840007	-3.122019	-0.836764	1.808899	1.797298	-2.920232	-0.376355	-1.871479	0.055867	0.043726	1.931029e-02	0.030143	0.047416	0.005468	0.004863	0.003194	0.001835	0.000984	0.000256	0.000517	0.000120	0.000568	0.000497	0.000414	0.000226	0.000100	0.000210	0.000277	18.729539	12.978474	0.389411	3.097491	1.653838	2.788992	-2.300185	-0.338623	1.053962	0.298855	2.201297	-2.190385	-2.114981	-2.855240	1.155340	-2.180461	-1.211002	-2.835941	-0.894978	1.239837	4.162230	4.393826	4.538836	4.232913	3.315121	0.845925	0.700195	0.744376	0.779161	0.909964	0.767153	0.733933	0.693420	0.804102	0.958531	0.000024	0.000012	0.000004	0.000005	0.000019	0.024806	-0.002134	0.003222	0.002783	-0.016505	0.387600	0.275675	0.178959	0.183813	0.280345	0.375000	0.416667	0.354167	0.382979	0.354167	0.096077	0.143660	0.163974	0.133535	0.122831	0.297264	0.288182	0.304214	0.211255	0.181013	0.470164	0.473413	0.405834	0.390981	0.297632	0.610263	0.627020	0.605184	0.608123	0.496641	0.818516	0.855191	0.798959	0.841186	0.766617	-2.227000e-05	0.000037	0.000025	0.000027	0.000046	0.129831	0.272989	0.118297	0.078878	0.367989	0.104694	0.095423	0.056949	0.057869	0.062551	0.375000	0.312500	0.354167	0.404255	0.437500	0.033333	-0.033333	0.033333	-0.166667	0.033333	0.384958	0.256928	0.179423	0.184840	0.283508	0.459124	0.400733	0.254357	0.237523	0.385478	1.291871	1.766413	0.508097	0.537821	0.044167	0.779065	1.430244	1.726261	1.268742	0.199607	0.082305	0.022619	0.058135	0.148859	0.233059	-0.031466	-0.481291	-0.337741	-0.079090	0.288235	0.161129	0.134317	0.085149	0.082704	0.123662	0.557973	0.287531	-0.353994	-0.366384	0.044065	0.992721	1.022364	1.022761	0.999441	0.954409	2.080271	2.255962	2.751496	2.809766	2.374753	11.164122	54.645052	25.415659	13.473346	1.332243	0.025338	0.018961	0.007272	0.006673	0.001101	1.370000e-06	1.030000e-06	4.000000e-07	3.700000e-07	6.000000e-08	0.341615	0.341128	0.331682	0.313442	0.175390	1.044377	0.891954	0.658078	0.793161	1.476852	0.021202	0.051148	0.012555	0.017048	0.024527	117.796541	15.694906	112.661792	47.760664	13.566240	0.082823
1468019	309.22200	-0.160658	-1.460134	-0.758934	0.396559	28501.385092	32930.588107	3.690130e+04	5.006247e+04	5.114888e+04	NaN	386.136291	158.283404	206.501385	304.426799	1114.186241	NaN	28380.031107	33401.401023	3.677471e+04	5.005832e+04	5.108732e+04	NaN	430.585253	205.464503	268.733668	393.686038	1212.454970	NaN	20.18258	20.105960	19.982310	19.651100	19.664880	NaN	0.014701	0.005218	0.006074	0.006600	0.023517	NaN	20.18721	20.090550	19.986040	19.651190	19.666180	NaN	0.016463	0.006677	0.007932	0.008536	0.025621	NaN	0.0	0.000000	0.000000	0.000000	0.000000	NaN	0.156834	0.123606	0.331176	0.023310	NaN	0.015608	0.008009	0.008973	0.024555	NaN	Qso	NaN	1.775506	0	0.0	0.0	0.0	0.0	<NA>	302	1117	52885	0.739633	0.177546	0.140664	0.000896	0.013523	1.195596e-02	213.720847	513.215165	507.257670	5045.111184	807.860345	0.510180	0.148918	0.135026	0.262679	0.123857	0.107137	0.012737	0.008008	0.029495	0.015843	0.002680	0.003516	0.001900	0.037808	0.005104	0.001790	0.000633	0.001074	0.014837	0.000850	0.000227	19.014730	2.000951	0.000255	2.000985	3.003659	2.593629	0.302106	3.035866	0.875070	2.049443	-1.855418	2.819227	1.287948	2.156429	2.677678	-0.190069	-0.134477	-0.095421	-0.463011	-1.510646	0.080189	0.052124	3.694239e-02	0.031140	0.073025	0.003267	0.005340	0.006792	0.001191	0.002444	0.000654	0.001059	0.000410	0.000569	0.000285	0.000473	0.000398	0.000093	0.000059	0.000305	0.359303	12.001477	24.550900	25.015358	29.612731	1.251305	1.677849	2.270504	0.986333	-2.201662	-0.065493	2.292986	2.532553	1.173995	-2.501912	-1.693122	-1.401796	0.623513	0.417805	-1.915202	0.070424	0.040987	2.662948e-02	0.023559	0.065085	0.007990	0.002874	0.002691	0.002274	0.002422	0.000152	0.000597	0.000207	0.000541	0.000551	0.000230	0.000052	0.000126	0.000070	0.000680	25.106844	11.520414	17.425787	3.454329	1.230420	2.078743	0.341660	1.992841	-1.442066	1.014817	0.651861	2.557126	-2.455214	0.409142	0.536271	1.779728	-2.460042	1.999164	0.806654	0.771572	3.954399	4.459454	4.556946	4.702675	3.785923	0.906044	0.791755	0.760617	0.743693	0.918898	0.936344	0.832485	0.681253	0.692148	0.937800	0.000029	0.000010	0.000006	0.000004	0.000025	0.008804	0.006156	-0.198535	0.009451	0.012395	0.442917	0.344234	0.329887	0.258027	0.367122	0.234043	0.304348	0.244444	0.266667	0.212766	0.114932	0.296504	0.237074	0.212644	0.158339	0.246375	0.415587	0.508037	0.388412	0.281504	0.373852	0.506396	0.701680	0.598051	0.383790	0.519567	0.619761	0.818352	0.725300	0.568516	0.761608	0.696090	0.927373	0.849069	0.679875	1.195800e-04	0.000113	-0.000009	0.000118	0.000112	0.384221	0.090891	0.079603	0.038247	0.228473	0.098904	0.081869	0.087105	0.067537	0.103928	0.468085	0.413043	0.400000	0.311111	0.361702	0.100000	0.166667	-0.033333	0.100000	-0.033333	0.619262	0.478787	0.527983	0.359395	0.459924	0.463822	0.329422	0.251868	0.241204	0.467768	1.132212	0.750777	0.649467	-0.199657	0.110392	0.487515	2.038575	1.977020	2.347024	0.776729	-0.464977	-0.812922	-1.134318	-0.979809	-0.361376	1.526545	1.824769	3.113470	2.371773	0.383052	0.169693	0.134184	0.133078	0.111634	0.152024	0.461012	0.166628	0.176335	-0.124444	0.407300	0.944166	1.022796	0.974918	0.963955	0.999051	1.964447	2.226100	2.199211	2.414888	2.087862	10.436658	42.737051	41.872080	25.045837	3.784576	0.025407	0.018023	0.018775	0.012841	0.010462	1.330000e-06	9.700000e-07	1.050000e-06	7.400000e-07	5.800000e-07	0.288936	0.348581	0.373660	0.375174	0.317573	1.491056	0.746232	0.614257	0.406169	1.064834	0.074849	0.232625	0.081062	0.066099	0.012657	11.044441	2.410207	20.050749	22.582279	423.371702	0.093687
1468020	309.21940	-0.479245	0.036148	-0.022135	-0.220993	17663.977528	25333.897183	3.227447e+04	3.182550e+04	4.002968e+04	NaN	398.222241	159.416918	209.279951	308.870174	1116.490649	NaN	17754.149854	25769.644397	3.277461e+04	3.282450e+04	4.067704e+04	NaN	429.966222	193.027958	263.115830	362.337906	1196.564096	NaN	20.70151	20.390630	20.127720	20.142670	19.929070	NaN	0.024440	0.006830	0.007038	0.010528	0.030004	NaN	20.69599	20.372120	20.111030	20.109140	19.911810	NaN	0.026254	0.008130	0.008713	0.011976	0.031653	NaN	0.0	0.000000	0.000000	0.000000	0.000000	NaN	0.391534	0.262893	-0.015210	0.249017	NaN	0.025413	0.009810	0.012673	0.032064	NaN	Qso	NaN	0.930411	0	0.0	0.0	0.0	0.0	<NA>	304	1117	52885	0.201489	1.363053	0.078490	0.000202	0.001060	1.361463e-04	89.415539	605.093270	46.875148	996.115480	2665.694906	1678.072774	0.467674	0.378533	0.329328	0.316324	0.283578	0.061129	0.067962	0.066512	0.054438	0.047644	0.020499	0.011226	0.011250	0.009613	0.013165	0.003942	0.005307	0.003884	0.003736	0.005010	1.000484	1.000518	0.000458	0.000424	0.000357	-3.005833	2.687900	-2.957755	-2.823840	-3.042463	1.608064	1.925203	1.391874	1.603074	1.322838	-1.757516	-1.761957	0.470010	0.207547	-0.495430	0.077616	0.038788	3.779340e-02	0.040390	0.059346	0.008382	0.002278	0.001225	0.002682	0.004746	0.001446	0.000924	0.000741	0.000506	0.001953	0.000247	0.000071	0.000156	0.000103	0.000114	1.525185	13.996638	15.734695	27.800304	14.636019	-0.878518	-2.006997	2.435140	-0.995988	-2.080720	2.053940	-2.156458	2.955940	0.846721	-0.422632	-1.645010	-1.433332	-0.428857	-0.402440	-3.135600	0.055498	0.028520	2.796580e-02	0.028851	0.047831	0.000503	0.002538	0.001461	0.000934	0.003186	0.000205	0.000204	0.000243	0.000307	0.001203	0.000130	0.000121	0.000140	0.000135	0.000059	23.960183	16.886483	13.154216	19.587992	3.487881	-1.566561	-1.331363	3.105135	-2.509633	2.047149	0.082870	0.867017	2.192659	2.089162	-0.750037	-1.626146	0.634092	1.067493	-0.125145	-3.044556	5.512748	5.617791	5.654212	5.316707	5.360982	0.541849	0.505166	0.541647	0.408227	0.591676	0.523773	0.502023	0.524704	0.374589	0.585923	0.000031	0.000011	0.000011	0.000027	0.000021	0.160885	0.088715	0.032551	0.015681	-0.012232	0.715081	0.699245	0.557713	0.653931	0.472645	0.403509	0.392857	0.421053	0.464286	0.403509	0.111188	0.078711	0.085343	0.094661	0.196502	0.420528	0.306760	0.180602	0.340417	0.369828	0.617246	0.651348	0.601022	0.628679	0.536724	0.764011	0.849869	0.860403	0.845367	0.765129	0.847504	0.937627	0.932652	0.925814	0.878853	3.768000e-05	0.000039	0.000014	-0.000035	-0.000048	0.316883	0.086682	0.157323	0.653931	0.469391	0.319454	0.271051	0.238239	0.252708	0.164942	0.280702	0.339286	0.403509	0.357143	0.280702	-0.033333	-0.033333	0.033333	0.233333	-0.033333	0.604388	0.589960	0.481529	0.559985	0.497787	0.969020	0.751218	0.719737	0.721179	0.663997	0.809259	1.191550	0.970749	1.478578	0.035316	1.953546	3.154672	3.219797	2.509459	1.701879	0.484382	0.616732	0.349345	0.506684	0.139214	-0.556336	0.064396	-0.487515	0.140554	-0.827155	0.382094	0.309613	0.270636	0.288729	0.236794	2.716274	1.953879	1.592260	1.783280	1.470895	1.010060	0.991875	0.995434	0.993235	1.054099	1.214309	1.430231	1.519230	1.470553	1.637130	14.678501	109.462036	103.482726	70.572294	6.726001	0.159873	0.103512	0.079506	0.089199	0.045368	6.830000e-06	4.590000e-06	3.560000e-06	4.060000e-06	2.070000e-06	0.364368	0.380877	0.379780	0.318925	0.384659	0.526571	0.304362	0.252411	0.887076	0.589323	0.032150	0.024506	0.017833	0.046360	0.010816	246.515970	319.834034	446.851609	82.040181	742.588577	0.132956
1468021	309.21640	0.516741	-0.306719	-0.511302	1.150066	25982.198589	31090.684004	3.381537e+04	4.482806e+04	4.863596e+04	NaN	750.565014	316.157364	439.970387	654.381326	2178.868855	NaN	26002.322269	31301.339295	3.367639e+04	4.461995e+04	4.856614e+04	NaN	816.941358	362.905065	497.835096	736.317811	2284.366625	NaN	20.28299	20.168370	20.077100	19.770960	19.719250	NaN	0.031342	0.011038	0.014122	0.015842	0.048335	NaN	20.28215	20.161040	20.081570	19.776010	19.720800	NaN	0.034087	0.012585	0.016045	0.017909	0.050748	NaN	0.0	0.000000	0.000000	0.000000	0.000000	NaN	0.194886	0.091210	0.306090	0.088519	NaN	0.033251	0.017929	0.021231	0.051158	NaN	Qso	NaN	1.641482	0	0.0	0.0	0.0	0.0	<NA>	356	1117	52885	87.331947	0.455384	0.009274	0.487933	0.002650	3.954635e+01	29019.253221	121.892581	0.583733	21212.673164	1154.429673	381.368921	0.185746	0.142586	0.125577	0.086346	0.096046	0.024166	0.014164	0.014224	0.004410	0.008721	0.007687	0.002552	0.002201	0.001064	0.001064	0.001152	0.001228	0.000778	0.000334	0.000362	10.369730	0.001511	0.001511	2.001102	32.355523	-0.578047	0.670894	0.608868	-2.935889	1.537759	0.477211	-2.778425	-2.683634	2.538220	-2.155682	1.435024	-0.596669	-1.084921	-0.203170	0.317129	0.136412	0.048719	4.523347e-02	0.042792	0.070974	0.005474	0.001972	0.004130	0.000825	0.004541	0.002917	0.000937	0.001345	0.001391	0.000524	0.000074	0.000108	0.000311	0.000162	0.000473	31.350804	15.027802	11.801712	16.336110	7.939783	-3.132334	0.467444	-0.843457	1.828313	1.929485	-2.793311	2.971472	-2.733785	-0.311132	-0.603712	-0.315200	-0.416470	1.831915	-0.494099	-1.213493	0.103838	0.046216	3.082267e-02	0.031983	0.070274	0.006652	0.001718	0.002389	0.002858	0.002957	0.001790	0.000426	0.000370	0.000571	0.001999	0.000215	0.000200	0.000132	0.000099	0.000614	26.406959	21.932414	25.828718	16.015237	14.619067	2.396828	-1.310914	-0.157029	-0.753789	2.385869	-2.034262	-2.682885	-1.855232	-2.283703	-3.093259	2.061525	-2.248568	-0.475976	-1.029674	-2.353805	3.254399	4.348755	4.921343	4.676013	3.513592	1.040605	0.603822	0.664049	0.729843	0.990394	0.957009	0.645990	0.616292	0.761059	1.086557	0.000095	0.000026	0.000009	0.000007	0.000030	0.008344	0.008239	0.007698	0.002458	0.014540	0.731115	0.560903	0.288764	0.223940	0.367094	0.384615	0.500000	0.442308	0.346154	0.288462	0.092799	0.311724	0.271543	0.263179	0.144069	0.235159	0.422835	0.410175	0.355693	0.238366	0.352052	0.591136	0.510734	0.489278	0.315606	0.559109	0.716898	0.666865	0.579383	0.522876	0.794516	0.794905	0.833896	0.844275	0.734778	-1.339700e-04	0.000016	0.000022	0.000008	-0.000040	0.470631	0.420191	0.105783	0.250053	0.274826	0.159351	0.137753	0.099425	0.070849	0.080482	0.461538	0.423077	0.230769	0.269231	0.461538	-0.100000	0.100000	0.100000	0.033333	0.166667	1.310738	0.767167	0.291525	0.251764	0.444341	0.852881	0.406513	0.334311	0.281963	0.448147	2.134610	1.741194	0.904683	0.386733	0.549056	0.435475	1.639174	1.557181	1.422404	0.119644	-0.581331	-0.287372	0.576100	0.733402	-0.414401	1.073162	2.158302	0.071514	0.358642	0.892382	0.277390	0.184073	0.130033	0.106666	0.146794	1.546435	0.780892	0.228642	-0.173903	0.211476	0.943318	1.000520	1.035674	1.027725	0.950415	1.306777	1.875202	2.348189	2.580402	2.102024	14.650072	33.713166	15.707197	6.431842	2.174413	0.071851	0.033459	0.016688	0.010234	0.008980	3.350000e-06	1.580000e-06	7.900000e-07	5.000000e-07	4.400000e-07	0.245788	0.301959	0.413211	0.384396	0.167666	1.348739	1.426552	0.683760	0.866828	1.833954	0.152039	0.053163	0.020922	0.010311	0.046209	5.759539	14.565944	46.401780	88.653421	9.151643	0.073914

212425 rows × 384 columns

##FIND quasars indices and transform to arrays
setindexnew=data_manager.get_qso(setindexqso)
setindexnew=np.array(setindexnew)
df = pd.DataFrame({'objectId': setindexnew})
df.set_index('objectId', inplace=True)
setidnew=df.index

from QhX.light_curve import  get_lc22

Load u,g,r,i light curve of Object ID=1384142, light_cruves_data as stacked array

get_lc22 Function Overview

The get_lc22 function processes and returns light curve data :

Input Parameters: - data_manager: An object containing the light curve data, organized for retrieval by set IDs. - set1: A string identifier for the object whose light curves are to be processed. It selects the specific dataset within data_manager. - include_errors (optional): A boolean flag to decide whether magnitude errors should be included in the time series data. Defaults to True. Process Flow: 1. Data Validation: Checks if the specified set1 ID exists within data_manager. If not, it exits with None, indicating an error or absence of data. 2. Data Extraction: Retrieves and processes data for each filter (assumes filters range from 1 to 4), sorting by Modified Julian Date (mjd) and removing any null values. 3. Outlier Removal: Uses outliers_mad function to cleanse the light curve data, considering magnitude errors if they are to be included and available. 4. Data Augmentation and Sampling: If magnitude errors are present and requested, we add observational errors to the light curves by perturbing each data point within its error margin: (N(0,err_mag)). It enables period-finding algorithm to account for the uncertainty in each data point, leading to a more accurate and reliable estimation of the object’s periodicity. The function calculates the sampling rate for each filter’s time series as the mean difference between consecutive time points.

Output: The function outputs a tuple containing: - Processed time series data for each filter, with or without magnitude errors, based on the include_errors flag. - The respective sampling rates for each filter’s data, providing insight into the time resolution of the observations.

This comprehensive processing and return of light curve data allow for an in-depth analysis of astronomical objects, taking into account data quality and observational errors.

light_curves_data = get_lc22(data_manager, '1384142', include_errors=False)

light_curves_data

(array([51818.43, 52171.42, 52173.4 , 52224.38, 52234.33, 52283.17,
        52287.18, 52557.47, 52585.37, 52908.45, 52912.43, 52934.38,
        52936.37, 53270.44, 53272.49, 53286.46, 53288.41, 53294.46,
        53296.41, 53298.46, 53312.37, 53314.37, 53616.47, 53639.48,
        53657.44, 53675.38, 53680.39, 53686.39, 53699.41, 53989.47,
        54008.46, 54009.42, 54011.48, 54025.48, 54029.49, 54031.4 ,
        54036.41, 54039.4 , 54041.37, 54048.43, 54052.4 , 54058.4 ,
        54060.42, 54065.4 , 54365.47, 54381.49, 54386.48, 54392.48,
        54393.49, 54396.35, 54403.4 , 54404.46, 54406.39, 54409.4 ,
        54412.42, 54416.39, 54421.4 , 54423.38, 54433.4 ]),
 array([19.487167, 19.258741, 19.26747 , 19.273075, 19.276268, 19.24133 ,
        19.18076 , 19.29091 , 19.317068, 19.309761, 19.27774 , 19.258095,
        19.270597, 19.218782, 19.211699, 19.385593, 19.248219, 19.244982,
        19.233717, 19.230547, 19.160337, 19.168606, 19.263157, 19.48252 ,
        19.205746, 19.189566, 19.186361, 19.186861, 19.259214, 19.435116,
        19.442768, 19.454254, 19.433054, 19.262674, 19.41067 , 19.416674,
        19.461267, 19.449898, 19.428154, 19.509014, 19.470942, 19.426008,
        19.519487, 19.488789, 19.492743, 19.55684 , 19.496195, 19.485415,
        19.53713 , 19.458233, 19.49737 , 19.566244, 19.460844, 19.478912,
        19.502745, 19.518599, 19.503729, 19.47426 , 19.51499 ],
       dtype=float32),
 array([51818.43, 52171.42, 52173.39, 52224.37, 52234.33, 52283.16,
        52287.17, 52557.47, 52585.37, 52908.44, 52912.42, 52934.37,
        52936.37, 53270.43, 53272.48, 53286.45, 53288.41, 53294.46,
        53296.41, 53298.46, 53312.36, 53314.36, 53616.47, 53639.48,
        53657.43, 53675.38, 53680.39, 53686.39, 53699.41, 53989.47,
        54008.45, 54009.42, 54011.48, 54025.48, 54029.49, 54031.4 ,
        54036.4 , 54039.4 , 54041.37, 54048.42, 54052.4 , 54058.39,
        54060.42, 54065.39, 54365.47, 54381.49, 54386.48, 54392.48,
        54393.49, 54396.35, 54403.4 , 54404.45, 54406.39, 54409.4 ,
        54412.42, 54416.39, 54421.4 , 54423.37, 54433.4 ]),
 array([19.067541, 18.858826, 18.87784 , 18.88775 , 18.880558, 18.835482,
        18.865055, 18.896397, 18.906034, 18.986784, 18.88963 , 18.897112,
        18.927052, 18.85413 , 18.81973 , 19.044624, 18.863712, 18.783983,
        18.863485, 18.807205, 18.87544 , 18.788204, 18.839628, 18.849302,
        18.83286 , 18.788876, 18.834482, 18.84284 , 18.844952, 19.043533,
        19.01445 , 19.01894 , 18.994421, 18.941622, 19.008762, 19.013212,
        19.015945, 19.026535, 19.036034, 19.045956, 19.012663, 19.041765,
        19.041842, 19.056908, 19.090286, 19.117542, 19.071148, 19.06857 ,
        19.088623, 19.095001, 19.048058, 19.085863, 19.06356 , 19.091923,
        19.084703, 19.111233, 19.11881 , 19.13508 , 19.070162],
       dtype=float32),
 array([51818.43, 52171.42, 52173.4 , 52224.38, 52234.33, 52283.16,
        52287.18, 52557.47, 52585.37, 52908.44, 52912.42, 52934.38,
        52936.37, 53270.44, 53272.49, 53286.45, 53288.41, 53294.46,
        53296.41, 53298.46, 53312.36, 53314.36, 53616.47, 53639.48,
        53657.44, 53675.38, 53680.39, 53686.39, 53699.41, 53989.47,
        54008.45, 54009.42, 54011.48, 54025.48, 54029.49, 54031.4 ,
        54036.4 , 54039.4 , 54041.37, 54048.42, 54052.4 , 54058.39,
        54060.42, 54065.39, 54365.47, 54381.49, 54386.48, 54392.48,
        54393.49, 54396.35, 54403.4 , 54404.46, 54406.39, 54409.4 ,
        54412.42, 54416.39, 54421.4 , 54423.37, 54433.4 ]),
 array([18.845848, 18.71427 , 18.717072, 18.706953, 18.738094, 18.702692,
        18.740034, 18.746946, 18.708296, 18.777199, 18.768492, 18.742142,
        18.755127, 18.704638, 18.696827, 18.824139, 18.677223, 18.703337,
        18.70635 , 18.627716, 18.691744, 18.642471, 18.712446, 18.715885,
        18.677671, 18.625593, 18.631302, 18.669907, 18.707012, 18.857832,
        18.839558, 18.86638 , 18.834661, 18.829254, 18.856771, 18.861313,
        18.846321, 18.858253, 18.819777, 18.835802, 18.847778, 18.821941,
        18.866451, 18.854805, 18.887213, 18.888792, 18.89962 , 18.913237,
        18.886803, 18.959562, 18.899456, 18.920807, 18.937399, 18.902845,
        18.905334, 18.906374, 18.87291 , 18.94068 , 18.890202],
       dtype=float32),
 array([51818.43, 52171.42, 52173.4 , 52224.38, 52234.33, 52283.16,
        52287.18, 52557.47, 52585.37, 52908.45, 52912.42, 52934.38,
        52936.37, 53270.44, 53272.49, 53286.46, 53288.41, 53294.46,
        53296.41, 53298.46, 53312.37, 53314.37, 53616.47, 53657.44,
        53675.38, 53680.39, 53686.39, 53699.41, 53989.47, 54008.46,
        54009.42, 54011.48, 54025.48, 54029.49, 54031.4 , 54036.4 ,
        54039.4 , 54041.37, 54048.42, 54052.4 , 54058.4 , 54060.42,
        54065.4 , 54365.47, 54381.49, 54386.48, 54392.48, 54393.49,
        54396.35, 54403.4 , 54404.46, 54406.39, 54409.4 , 54412.42,
        54416.39, 54421.4 , 54423.37, 54433.4 ]),
 array([18.532455, 18.413788, 18.492144, 18.384977, 18.39705 , 18.365591,
        18.416399, 18.44976 , 18.381535, 18.4777  , 18.405382, 18.376106,
        18.459177, 18.387926, 18.42326 , 18.460321, 18.359886, 18.458498,
        18.391264, 18.349352, 18.355343, 18.313208, 18.453217, 18.363897,
        18.342276, 18.337543, 18.306156, 18.479729, 18.480738, 18.448893,
        18.487144, 18.43134 , 18.416773, 18.557781, 18.436623, 18.471283,
        18.505116, 18.482761, 18.548965, 18.562773, 18.532354, 18.487179,
        18.559294, 18.510853, 18.576326, 18.538883, 18.51235 , 18.605324,
        18.49462 , 18.552446, 18.461958, 18.53137 , 18.572111, 18.537954,
        18.521812, 18.542027, 18.555769, 18.512682], dtype=float32),
 45.08568965517243,
 45.08568965517243,
 45.08568965517243,
 45.87666666666669)

from QhX.calculation import periods, signif_johnson

import numpy as np
from QhX.light_curve import get_lctiktok, get_lc22
from QhX.calculation import *
# Ensure to import or define other necessary functions like hybrid2d, periods, same_periods, etc.
from QhX.algorithms.wavelets.wwtz import *

# Retrieve light curves as separate arrays, using the get_lc22 function with include_errors parameter
tt0, yy0,tt1, yy1, tt2, yy2, tt3, yy3, sampling0, sampling1, sampling2, sampling3 = get_lc22(data_manager, '1384142', include_errors=True)

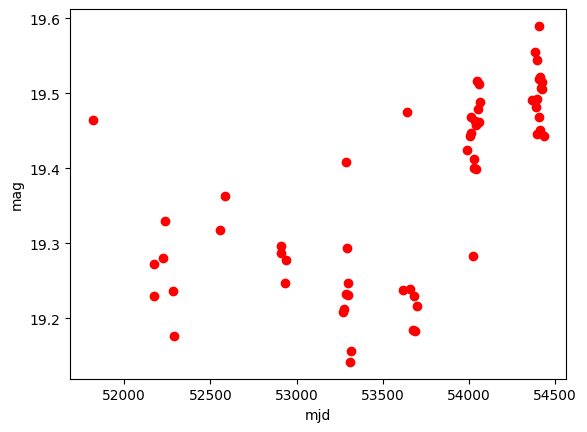
plt.plot(tt0,yy0,'ro')
plt.ylabel('mag')
plt.xlabel('mjd')

Text(0.5, 0, 'mjd')

Simple version of paralelization of objects processing. Calculation of wavelet matrices for each light curve is paralelized in the libwwz library

from QhX.processing_utils  import parallel_pool
#Note: parallel_pool supports two modes—fixed and dynamical. The default mode is fixed.
#Please refer to the module documentation for further details.
# Example set IDs and parameters for the processing function
setids = ['1385092', '1385097', '1385098']
#    data_manager = DataManager()  # Presumed to be a previously defined DataManager instance

    # Parameters for the processing function
ntau = 80
ngrid = 80
provided_minfq = 200
provided_maxfq = 10
include_errors = False

    # Execute the parallel processing function and print the results
results = parallel_pool(setids, data_manager, ntau, ngrid, provided_minfq, provided_maxfq, include_errors, num_threads=3)

*** Starting Weighted Wavelet Z-transform ***

adjusted time_divisions to:  63
Pseudo sample frequency (median) is  0.2
largest tau window is  42.177
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.5
largest tau window is  33.101
3.27 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

adjusted time_divisions to:  65
Pseudo sample frequency (median) is  0.201
largest tau window is  40.859
5.79 seconds has passed to complete Weighted Wavelet Z-transform

6.25 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.519
largest tau window is  33.101
2.8 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

adjusted time_divisions to:  65
Pseudo sample frequency (median) is  0.2
largest tau window is  40.702
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.503
largest tau window is  33.101
2.82 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

adjusted time_divisions to:  65
Pseudo sample frequency (median) is  0.2
largest tau window is  40.859
4.35 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.521
largest tau window is  33.101
3.26 seconds has passed to complete Weighted Wavelet Z-transform

4.0 seconds has passed to complete Weighted Wavelet Z-transform

8.25 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.5
largest tau window is  33.101
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.5
largest tau window is  33.101
4.05 seconds has passed to complete Weighted Wavelet Z-transform

4.01 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.498
largest tau window is  33.101
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
4.01 seconds has passed to complete Weighted Wavelet Z-transform

4.06 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.98 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.94 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.95 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.94 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.94 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.04 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.99 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.98 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.96 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.01 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.99 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.31 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.18 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.29 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.38 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.17 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.09 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.09 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.24 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.42 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.38 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.32 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.32 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.17 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.13 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.12 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.03 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.04 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.04 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101

1.97 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.04 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.03 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.03 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.99 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.07 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.03 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.05 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.04 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.98 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.0 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.96 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.95 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.95 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.03 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.06 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.95 seconds has passed to complete Weighted Wavelet Z-transform

# If this script is executed directly (rather than imported as a module), run a test
if __name__ == "__main__":
    # Example set IDs and parameters for the processing function
    setids = ['1385092', '1385097']
#    data_manager = DataManager()  # Presumed to be a previously defined DataManager instance

    # Parameters for the processing function
    ntau = 80
    ngrid = 80
    provided_minfq = 200
    provided_maxfq = 10
    include_errors = False

    # Execute the parallel processing function and print the results
    results = parallel_pool(setids, data_manager, ntau, ngrid, provided_minfq, provided_maxfq, include_errors, num_threads=2)
    for result in results:
        print(result)

*** Starting Weighted Wavelet Z-transform ***
*** Starting Weighted Wavelet Z-transform ***


Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
Pseudo sample frequency (median) is  0.5
largest tau window is  33.101
4.1 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.503
largest tau window is  33.101
4.28 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.519
largest tau window is  33.101
4.174.04 seconds has passed to complete Weighted Wavelet Z-transform

 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.5
largest tau window is  33.101
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.521
largest tau window is  33.101
4.0 seconds has passed to complete Weighted Wavelet Z-transform

4.06 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.498
largest tau window is  33.101
*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.5
largest tau window is  33.101
4.3 seconds has passed to complete Weighted Wavelet Z-transform

4.34 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.1 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.08 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.0 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.99 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.0 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.13 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.0 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.04 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.11 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.23 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.2 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.19 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.19 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.18 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.18 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.24 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.12 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.32 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.23 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.22 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.29 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.1 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.13 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.21 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.11 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.05 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.13 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.11 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.09 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.07 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.16 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.41 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101

2.12 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.07 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.07 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.07 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.05 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
1.98 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.02 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.12 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.23 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.21 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.08 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.14 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.19 seconds has passed to complete Weighted Wavelet Z-transform

*** Starting Weighted Wavelet Z-transform ***

Pseudo sample frequency (median) is  0.515
largest tau window is  33.101
2.23 seconds has passed to complete Weighted Wavelet Z-transform

[{'objectid': '1385092', 'sampling_i': 20.115076923076916, 'sampling_j': 20.271085271317837, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-1'}, {'objectid': '1385092', 'sampling_i': 20.115076923076916, 'sampling_j': 19.961603053435123, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-2'}, {'objectid': '1385092', 'sampling_i': 20.115076923076916, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-3'}, {'objectid': '1385092', 'sampling_i': 20.271085271317837, 'sampling_j': 19.961603053435123, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-2'}, {'objectid': '1385092', 'sampling_i': 20.271085271317837, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-3'}, {'objectid': '1385092', 'sampling_i': 19.961603053435123, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '2-3'}]
[{'objectid': '1385097', 'sampling_i': 20.429374999999993, 'sampling_j': 20.115153846153856, 'period': 161.61616161616163, 'upper_error': -1, 'lower_error': -1, 'significance': 1.0, 'label': '0-1'}, {'objectid': '1385097', 'sampling_i': 20.429374999999993, 'sampling_j': 21.259918699187, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-2'}, {'objectid': '1385097', 'sampling_i': 20.429374999999993, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-3'}, {'objectid': '1385097', 'sampling_i': 20.115153846153856, 'sampling_j': 21.259918699187, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-2'}, {'objectid': '1385097', 'sampling_i': 20.115153846153856, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-3'}, {'objectid': '1385097', 'sampling_i': 21.259918699187, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '2-3'}]

for result in results:
    print(result)

[{'objectid': '1385092', 'sampling_i': 20.115076923076916, 'sampling_j': 20.271085271317837, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-1'}, {'objectid': '1385092', 'sampling_i': 20.115076923076916, 'sampling_j': 19.961603053435123, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-2'}, {'objectid': '1385092', 'sampling_i': 20.115076923076916, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-3'}, {'objectid': '1385092', 'sampling_i': 20.271085271317837, 'sampling_j': 19.961603053435123, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-2'}, {'objectid': '1385092', 'sampling_i': 20.271085271317837, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-3'}, {'objectid': '1385092', 'sampling_i': 19.961603053435123, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '2-3'}]
[{'objectid': '1385097', 'sampling_i': 20.429374999999993, 'sampling_j': 20.115153846153856, 'period': 161.61616161616163, 'upper_error': -1, 'lower_error': -1, 'significance': 1.0, 'label': '0-1'}, {'objectid': '1385097', 'sampling_i': 20.429374999999993, 'sampling_j': 21.259918699187, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-2'}, {'objectid': '1385097', 'sampling_i': 20.429374999999993, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-3'}, {'objectid': '1385097', 'sampling_i': 20.115153846153856, 'sampling_j': 21.259918699187, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-2'}, {'objectid': '1385097', 'sampling_i': 20.115153846153856, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-3'}, {'objectid': '1385097', 'sampling_i': 21.259918699187, 'sampling_j': 21.25983739837398, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '2-3'}]
[{'objectid': '1385098', 'sampling_i': 42.176774193548376, 'sampling_j': 40.85890625000002, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-1'}, {'objectid': '1385098', 'sampling_i': 42.176774193548376, 'sampling_j': 40.702343749999955, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-2'}, {'objectid': '1385098', 'sampling_i': 42.176774193548376, 'sampling_j': 40.858749999999986, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '0-3'}, {'objectid': '1385098', 'sampling_i': 40.85890625000002, 'sampling_j': 40.702343749999955, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-2'}, {'objectid': '1385098', 'sampling_i': 40.85890625000002, 'sampling_j': 40.858749999999986, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '1-3'}, {'objectid': '1385098', 'sampling_i': 40.702343749999955, 'sampling_j': 40.858749999999986, 'period': nan, 'upper_error': nan, 'lower_error': nan, 'significance': nan, 'label': '2-3'}]

pp=process1_new(data_manager, '1385097', ntau=80, ngrid=800, provided_minfq=2000, provided_maxfq=10, include_errors=False)

results

process12_results=[[{'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.08568965517243,
  'period': 446.179587283882,
  'upper_error': 26.594480680527795,
  'lower_error': 22.513862402711993,
  'significance': 0.98,
  'label': '0-1'},
 {'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.08568965517243,
  'period': 446.179587283882,
  'upper_error': 35.654914195946844,
  'lower_error': 17.127186682281263,
  'significance': 1.0,
  'label': '0-2'},
 {'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.87666666666669,
  'period': 446.179587283882,
  'upper_error': 30.9002280462837,
  'lower_error': 20.398836831717233,
  'significance': 1.0,
  'label': '0-3'},
 {'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.08568965517243,
  'period': 472.39444936522017,
  'upper_error': 26.594480680527795,
  'lower_error': 22.513862402711993,
  'significance': 1.0,
  'label': '1-2'},
 {'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.87666666666669,
  'period': 472.39444936522017,
  'upper_error': 26.594480680527795,
  'lower_error': 22.513862402711993,
  'significance': 1.0,
  'label': '1-3'},
 {'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.87666666666669,
  'period': 308.999613750483,
  'upper_error': 22.17397677238779,
  'lower_error': 3.746728576973794,
  'significance': 0.98,
  'label': '1-3'},
 {'objectid': '1384142',
  'sampling_i': 45.08568965517243,
  'sampling_j': 45.87666666666669,
  'period': 472.39444936522017,
  'upper_error': 30.9002280462837,
  'lower_error': 20.398836831717233,
  'significance': 0.94,
  'label': '2-3'}]]

from QhX.output import classify_periods, classify_period

outt=classify_periods(results)

#outt is a table containing: ‘ID’: object name, ‘m3’: ‘Common period (found in Band1 & Band2)’] ‘m4’: ‘Lower error bound’,

‘m5’: ‘Upper error bound’,

‘m6’: ‘Significance (based on Johnson et al)’,

‘m7_1’: ‘Band1’,#usaully 0=u, 1=g,2=r,3=z

‘m7_2’: ‘Band2’,

‘period_diff’:difference of detected periods ‘iou’: inetrsection over union metric

#Each individual period in above table is classified based on these statistical criterions:

if row[‘m6’] >= 0.99 and rel_error_lower <= 0.1 and rel_error_upper <= 0.1 and row[‘iou’] >= 0.99 and consistent_period: return ‘reliable’ elif 0.5 <= row[‘m6’] < 0.99 and 0.1 < rel_error_lower <= 0.3 and 0.1 < rel_error_upper <= 0.3 and 0.8 <= row[‘iou’] < 0.99 and consistent_period: return ‘medium reliable’ else: return ‘poor’

# Assuming output_df is the DataFrame returned by classify_periods function
outt['classification'] =outt.apply(classify_period, axis=1)
print(outt)

   objectid          m3   m4   m5   m6 m7_1 m7_2  period_diff  iou  \
0   1385092         NaN  NaN  NaN  NaN  0-1  0-2          NaN  NaN
1   1385092         NaN  NaN  NaN  NaN  0-1  0-3          NaN  NaN
2   1385092         NaN  NaN  NaN  NaN  0-1  1-2          NaN  NaN
3   1385092         NaN  NaN  NaN  NaN  0-1  1-3          NaN  NaN
4   1385092         NaN  NaN  NaN  NaN  0-1  2-3          NaN  NaN
5   1385092         NaN  NaN  NaN  NaN  0-2  0-3          NaN  NaN
6   1385092         NaN  NaN  NaN  NaN  0-2  1-2          NaN  NaN
7   1385092         NaN  NaN  NaN  NaN  0-2  1-3          NaN  NaN
8   1385092         NaN  NaN  NaN  NaN  0-2  2-3          NaN  NaN
9   1385092         NaN  NaN  NaN  NaN  0-3  1-2          NaN  NaN
10  1385092         NaN  NaN  NaN  NaN  0-3  1-3          NaN  NaN
11  1385092         NaN  NaN  NaN  NaN  0-3  2-3          NaN  NaN
12  1385092         NaN  NaN  NaN  NaN  1-2  1-3          NaN  NaN
13  1385092         NaN  NaN  NaN  NaN  1-2  2-3          NaN  NaN
14  1385092         NaN  NaN  NaN  NaN  1-3  2-3          NaN  NaN
15  1385097  161.616162 -1.0 -1.0  1.0  0-1  0-2          NaN  NaN
16  1385097  161.616162 -1.0 -1.0  1.0  0-1  0-3          NaN  NaN
17  1385097  161.616162 -1.0 -1.0  1.0  0-1  1-2          NaN  NaN
18  1385097  161.616162 -1.0 -1.0  1.0  0-1  1-3          NaN  NaN
19  1385097  161.616162 -1.0 -1.0  1.0  0-1  2-3          NaN  NaN
20  1385097         NaN  NaN  NaN  NaN  0-2  0-3          NaN  NaN
21  1385097         NaN  NaN  NaN  NaN  0-2  1-2          NaN  NaN
22  1385097         NaN  NaN  NaN  NaN  0-2  1-3          NaN  NaN
23  1385097         NaN  NaN  NaN  NaN  0-2  2-3          NaN  NaN
24  1385097         NaN  NaN  NaN  NaN  0-3  1-2          NaN  NaN
25  1385097         NaN  NaN  NaN  NaN  0-3  1-3          NaN  NaN
26  1385097         NaN  NaN  NaN  NaN  0-3  2-3          NaN  NaN
27  1385097         NaN  NaN  NaN  NaN  1-2  1-3          NaN  NaN
28  1385097         NaN  NaN  NaN  NaN  1-2  2-3          NaN  NaN
29  1385097         NaN  NaN  NaN  NaN  1-3  2-3          NaN  NaN
30  1385098         NaN  NaN  NaN  NaN  0-1  0-2          NaN  NaN
31  1385098         NaN  NaN  NaN  NaN  0-1  0-3          NaN  NaN
32  1385098         NaN  NaN  NaN  NaN  0-1  1-2          NaN  NaN
33  1385098         NaN  NaN  NaN  NaN  0-1  1-3          NaN  NaN
34  1385098         NaN  NaN  NaN  NaN  0-1  2-3          NaN  NaN
35  1385098         NaN  NaN  NaN  NaN  0-2  0-3          NaN  NaN
36  1385098         NaN  NaN  NaN  NaN  0-2  1-2          NaN  NaN
37  1385098         NaN  NaN  NaN  NaN  0-2  1-3          NaN  NaN
38  1385098         NaN  NaN  NaN  NaN  0-2  2-3          NaN  NaN
39  1385098         NaN  NaN  NaN  NaN  0-3  1-2          NaN  NaN
40  1385098         NaN  NaN  NaN  NaN  0-3  1-3          NaN  NaN
41  1385098         NaN  NaN  NaN  NaN  0-3  2-3          NaN  NaN
42  1385098         NaN  NaN  NaN  NaN  1-2  1-3          NaN  NaN
43  1385098         NaN  NaN  NaN  NaN  1-2  2-3          NaN  NaN
44  1385098         NaN  NaN  NaN  NaN  1-3  2-3          NaN  NaN

   classification
0             NAN
1             NAN
2             NAN
3             NAN
4             NAN
5             NAN
6             NAN
7             NAN
8             NAN
9             NAN
10            NAN
11            NAN
12            NAN
13            NAN
14            NAN
15            NAN
16            NAN
17            NAN
18            NAN
19            NAN
20            NAN
21            NAN
22            NAN
23            NAN
24            NAN
25            NAN
26            NAN
27            NAN
28            NAN
29            NAN
30            NAN
31            NAN
32            NAN
33            NAN
34            NAN
35            NAN
36            NAN
37            NAN
38            NAN
39            NAN
40            NAN
41            NAN
42            NAN
43            NAN
44            NAN

outt

import os, holoviews as hv
os.environ['HV_DOC_HTML'] = 'true'

from QhX.plots import interactive_plt

interactive_plt.create_interactive_plot(outt)